Addresses 
No. 11 is called the "address" of the coded number kept there. The word "address" has been borrowed from the Post Office and it has just the same meaning. Electronic computing without addresses is impossible. Naturally, the machine must know just where it has to store its numbers and where it can find them afterwards. (For example, it sends its intermediate results one after the other to "address 1," "address 2" and so on, and after that it needs only to call out: "Send the intermediate result of address 11 to my arithmetic unit!" or "Send the number of address 34 to my arithmetic unit!" It then gets the correct figures and can go on adding.)
At this point, however, we must make a short supplementary note to keep the record straight. The storage matrices are in reality larger than in our drawing. Not much can be achieved with the 16 cores we allocated to a matrix. Still, a matrix measuring 10 by 6 inches (or, in quite modern apparatus, no more than 5 by 2 inches) holds 1,000 cores. A "tower" of 35 matrices, such as is needed for calculating in numbers with seven digits, thus contains 35,000 hand-threaded rings. It is capable of storing 1,000 numbers, in other words, of showing 1,000 addresses. So the electronic computer will - we are compelled to make a correction - never call out, "Send me the number of address 11!" Instead, it will always state a four-figure number - 4711 for example. In this case, the 4 indicates the number of the tower, and the three figures following it refer to core 711 in each of the 35 matrices of tower No. 4.
Now you can forget that item of information for the time being. We shall turn once more to the five 16-core matrices in this illustration. They will provide us with enough to think about in the moment. For instance: how does one get the pulses of a coded number into the matrix and - this seems even more complicated - how does one get them out again?
Magnetizing-in is no great problem. We have already mentioned the procedure used: two half-pulses to wires "c" and "g" and, so on. If the coded number "10010" is to be brought to address 11 in the core storages of our drawings, we connect the wires "c" and "g" in each of the five matrices to the five leads on which the pulse "10010" arrive, as the following illustration shows.
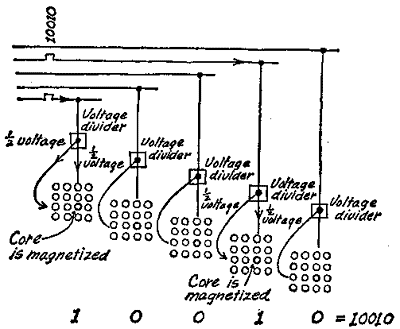
Only the first and the fourth matrices are reached, each by a total of one full pulse, which magnetizes the No. 11 cores and changes them from "0" to "I." The No. 11 cores of the other three matrices stay at "0." The "10010" is now well taken care of in the storage.
But how do we get them out again if the arithmetic unit needs them? For that purpose we need another wire about which we have said nothing until now. It is the "reading wire," a long metal thread which runs through the matrix diagonally in several turns and passes through each ring core:
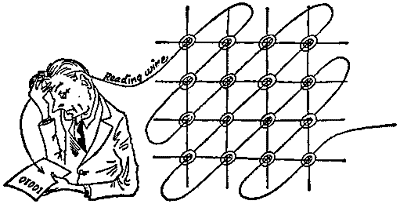
The arithmetic unit anxious to know what is in address 11 now does something quite remarkable: it applies half a negative pulse in each case to the leads "c" and "g" of all the matrices. In this way, all five ring cores containing No. 11 have two half negative pulses - in other words, one complete pulse - driven into their works.
The consequences are catastrophic as far as the cores magnetized to "1" are concerned. Their magnetization is canceled, the cores an demagnetized, they jump from "1" back to "0."
The other three, the cores unmagnetized from the start, are quite unaffected by the negative pulse. They stay at "0."
Well, what happens now? All cores with address 11 are now back at "0." The "10010," formerly so cunningly magnetized, has now been just as artfully spirited away. It has gone. Was that the idea?
No. But there was no other way of going about it. The great reading trick has already been achieved, as a matter of fact. Note well: the magnetized cores, when they are demagnetized, have "induced" electrically - so we say - a pulse in the reading wire. The electric energy in the magnetized rings had to escape somewhere when the negative pulse pressed it. It fled into the reading wire. Now it appears at its end as a correct, positive, normal pulse. A faultless "10010" actually has emerged from the five reading wires. It needs only to be forwarded to the arithmetic unit.
Did you get it? The principle is ingenious! You may raise the objection that this is all very well, but that it involves the disappearance of the stored information from the storage. All the participating ring cores are at "0" and there is nothing more to be found there.
You are quite right. But that is something one just has to put up with. However, the time during which all the cores are at "0" is a mere millionth of a second, no more. For, even while the pulses from the reading wires are, hurrying into the arithmetic unit, a small portion of their energy is being diverted, reinforced by transistors and remagnetized into the old address.
The core storages have many advantages, particularly an account of their high speed, and they me called on for tasks in working storages, even in auxiliary storages, which only a few years ago were entrusted only to magnetic drums. The "ER 56" electronic computer has room in its core storages for 9,000 seven-digit numbers. The "7090" of International Business Machines can accommodate up to 64,000 numbers in its core storages. The fact that the devices, because of their many ring cores, are tremendously expensive cannot be helped.

Flip-Flops >>>>
©
by PhiloPhax & Lauftext
& Redaktion Lohberg
Kybernetik
- Was ist das?
First printed in Germany: 1963