Every Memory is Magnetic
Has it ever occurred to you how close the connection is between thought and memory? Obviously, when one reflects on it, thinking is hardly possible at all without recollection, mental activity inconceivable without memory cells. That is why we use the word "re-mind" to mean "to came to remember, to recall to memory."
That applies to machines as well as to human beings.
You will remember that in calculating in the last chapter, numbers were stored before they were added. Intermediate results were kept in storages, and eventually the total was also put up in a storage before it came to light.
Storages
These repositories represent the memory of the electronic computer, and they are in fact often called "memories" as well as "stores" or "storages." Without them, it cannot think or solve mental problems. The storages have to take care of the results of sums, formulas, columns; of figures and rates of exchange, discounts, angle functions, the rules of Latin grammar and all bank accounts from Amos to Zymons. The bigger the capacity of a storage - the more capacious its memory - the more problems it can solve, and the more complicated are the problems it can solve. And, of course, the more expensive it will be.
Unlike a human memory, which is not always open to a full inspection (and is not always completely reliable) the storages of an electronic computer can be neatly divided up into absolutely leakproof compartments. There are input storages and output storages, for example. They receive the numbers with which a calculation is to be made, and make a note of the results before these are typed by the teleprinters on a sheet of paper.
Another compartment is formed by the intermediate storages. They keep a firm grip on the intermediate results the machine will need again for its future calculations. A special type of intermediate storage is the "accumulator," which is securely built into the arithmetic unit. The task of the accumulator is to receive the intermediate totals and to return them immediately to the matrix - together with the next number to be added. The accumulator also stores the units, tens and hundreds, while the matrix counts through from digit to digit.
No accumulator is actually necessary for binary counting. The calculating flip-flops are themselves fully capable of holding the intermediate results - by means of their switch position, which shows either "0" or "1." But occasionally accumulators are used even in such cases.
The intermediate storages, and thus the accumulator too we "short storages" or "high-speed storages" which need only hold their numbers or characters for a few moments - sometimes only for fractions of a second. They must be able to receive the information quickly and send it off again just as quickly, for their working speed most suit that of the arithmetic unit. The experts call all such high-speed storages "registers," and they among the most expensive components in the whole computer.
There are also "working storages" or "working memories." These expressions are rather vague, and might mean more or less anything. They are therefore quite suitable terms for their purpose, for the definition of a working storage has no firm outlines. The working memories take note of all those things which neither the input storages nor the output storages or registers are concerned with. As so often happens, these spheres of interest without any sharply defined limits are, in fact, the most extensive of all. In commercial computers, for example, rates of exchange and scales of discounts, taxation tables and pay rates are noted; and the working memory is the place where scientific computers keep their formulas, coefficients and mathematical functions.
The great jungles of data, however - the current accounts of the bank or mail order business, the whole ballast of scientific tables, the dictionaries of the translating machines - are relegated to "auxiliary storages." The auxiliary storage is the great library, the records office and sometimes also the warehouse of the electronic computer.
This Illustration shows you how the various storages relate to each other and to the arithmetic unit:
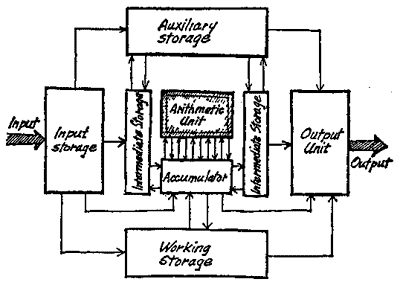
But we must regard this drawing as really nothing more than a rough sketch, as a way of showing how work is distributed inside the electronic memory. For the various storages in a computer are seldom marked off so distinctly from one another. Input storages, output storages and working storages are often a single unit; auxiliary storages and working storages frequently cannot be separated; in short, our sketch is a theoretical model rather than a practical representation. In practice, matters proceed in a much less clearly surveyable manner.
One of the reasons is that there are many ways of storing electronic information, and the best methods are so expensive that they are reserved for the most important parts of the computers memory. As for cheap methods of storage ... well, consider our familiar punched tapes again. Three hundred yards of them, with characters properly punched in, would make a really first-class memory, and a cheap one too. But punched tapes are just not fast enough to think with.
Magnetic tapes are much quicker, but they too are still in the slow-coach or pedestrian category. As auxiliary storages they are splendid, because their mental capacity is almost unlimited. A hundred yards of magnetic tape, more or less, can accept the bookkeeping of whole businesses, many-figured logarithmic tables and voluminous libraries of scientific data. But their access time is pretty long.
Access Time >>>>
©
by PhiloPhax & Lauftext
& Redaktion Lohberg
Kybernetik
- Was ist das?
First printed in Germany: 1963