Codes
Now we have cleared up the electrical side, to start with. Next we must see how we can join up the various ways of carrying out switching operations so that we can begin calculating. However, perhaps we should say a few words before-hand about the code in which we are going to count. We could of course take the teleprinter code we know already. But we have another code in mind. A (2/5) code. It looks really scientific, that (2/5). The (n/5 ) code we have had before ... ? No. We must explain that first of all.
The teleprinter, you see, codes the 2 as "10011" in the list, the 5 as "10000" and the 8 as "00110." Sometimes the codified numbers contain two "l"s, sometimes four, sometimes only one. The number of "1"s is indefinite, it is "n" as mathematicians say. That is why they call a five-channel code with an indefinite number of "i"s an (n/5 ) code, to be read "n-out-of-five code." We would prefer, however, to go over to a code in which the "1" in each sign turns up twice only-in other words to a (2/5) code, pronounced "two-out-of-five code."
Such a code could - if we now think in terms of numbers, not of letters or type symbols - have the following appearance:
| 0 = 00011 1 = 00101 2 = 00110 3 = 01001 4 = 01010 |
5 = 01100 6 = 10001 7 = 10010 8 = 10100 9 = 11000 |
If we count with this code on the following pages, we shall find ourselves in good company - for example, in that of the basic computers, such as the "ER 56" computer.
Illus. 15
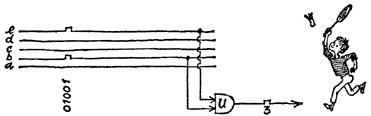
So now we can really get moving. Imagine yourself to be very small and creep with us into the arithmetic unit (Illus. 15). You will first of all see the five parallel leads on which the pulses from the punched-tape reader or from the magnetic tape make their way. To provide a better view, we write the letters "a" to "e" on the five wires. Number 3 (in the form of "01001") arrives over the punched tapes. We direct the pulse immediately into our five wires. You will recognize them as the "bridges" or kinks in the wires whose acquaintance you made in the previous chapter.
Now we must try to make a single pulse, which Will mean "3," out of the pulses of "01001." This presents no problem. What, after all, are our and-gates there for? We take one of them out of the drawer and connect its two control lines to wires "b" and "e." In our drawing, that has already been done. What happens? The two "I"s of "01001" branch off into the control lines, make their way into the and-gate, and cause a fresh pulse in their output lead. This is equivalent to the number 3.
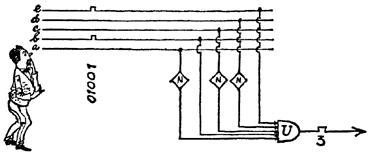
Our circuit functions superbly. But in practice, for safety's sake, it is done in a more complicated fashion in fact like this:
Illus. 16
©
by PhiloPhax & Lauftext
& Redaktion Lohberg
Kybernetik
- Was ist das?
First printed in Germany: 1963