Negaters
The three built-in negaters see to it that where no Pulse at all is allowed to arrive on the wires in the case of a "01001," one such pulse will turn up nevertheless.
In such a combination the and-gate is only allowed to respond when five pulses arrive on it at the same time.
Is the expense of the three negaters unnecessary or even a ridiculous waste of money? Well, as long as everything proceeds faultlessly, they are not absolutely indispensable. But suppose that as a result of some fault, some mistake, some stupid accident, a "11001" sign were to arrive. No provision has been made for that in the code. Without negaters, the and-gate for "T' would respond to it, and at the same time so would the and-gate intended to extract the "6' ("10001") and even the and-gate for "9" ("11000"). The result would be a pretty mix-up.
In this case, however, in our and-gate for "3," the negater connected with wire "a" would make an V' out of the wrong "I" pulse arriving on wire "a." The andgate reacting only to five "I" pulses would not respond. Nor would the and-gates for 'Y and "9" react. The machine would simply stop counting - you would be able to look for the fault and make a fresh start.
We will ask you to imagine in future that such negaters are built into all and-gates and or-gates. In order not to overload our drawings, we shall leave them out from now on.
And for every number from 0 to 9 we shall solder an and-gate in each case to our five wires - in Illus. 17.
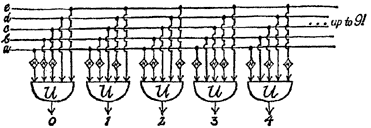
Illus. 17
Let us do it again (Illus, 18), taking five wires (which we shall call "f," "g," "h," "i" and "k") and attaching ten further and-gates. Then we arrange the output leads of the first ten and-gates neatly parallel to each other, and lay the output leads of the other ten and-gates crosswise over them. The result will look like this:
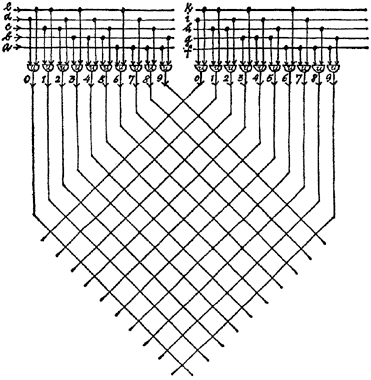
Illus. 18
Pretty to look at isn't it? But we are not concerned with its beauty. We are building an "adder matrix."
©
by PhiloPhax & Lauftext
& Redaktion Lohberg
Kybernetik
- Was ist das?
First printed in Germany: 1963