Graphics
You think this is a childish sort of game? Please don't. As a matter of fact what we are concerned with is practically science! Let us carry on with the game. How would it be if we were to put it in the form of drawing? We could make a graphic representation of finding one card in 32: first of all we show the pack containing 32 cards; then we show it divided into two heaps, etc ... You see the result in this Illustration.
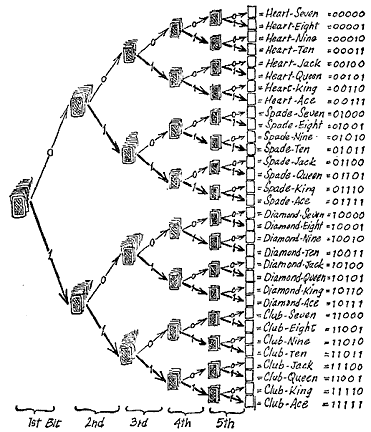
Our artistic exercise looks curious, almost like the top of a felled tree. You might perhaps call it "The Tree of KnowIedge". A "tree" is what it is in fact caIled hy the cxperts.
We have now left the world of games and stumbled into the realm of science, where there are whole forests of such trees. Let us check graphically how we found the Jack of Diamonds among the boughs.
If the cards are arranged in just the same way as the leaves in the tree, the answers must be "Lower stack - upper stack - lower stack - upper stack - upper card."
As you will notice, we have drawn the limbs of the tree, the arrows, in varying thicknesses. We could also find the Jack of Diamonds by saying: "Thick arrow - thin arrow - thick arrow - thin arrow - thin arrow."
That sounds like a counting-off rhyme used by the Sioux Indians. So we shall put it more briefly and say, instead of "thin arrow" and "Thick arrow", just "0" and "1". Expressed in this fashion, the way to the Jack of Diamonds would be "10100." We could go still farther and say that we shall call the Jack of Diamonds himself "10100." We shall call the Ace of Hearts "00111," the King of Spades "01110" and the Ace of Clubs "11111."
If you happen to have an information theoretician near at hand, ask him what he thinks about your Calling the Jack of Diamonds "10100."
"Well?" he would teIl you, "you've simply applied a binary code to the playing cards."
You see? You have actually succeeded in doing something scientifically acceptable.
"You have assigned a code, a system of symbols, to a deck of playing cards," the information speciallst would explain, "the word 'binary' meaning that this code consists of only two symbols - '0' and '1'."
From the. questions "upper stack?" and "lower stack?" and the answers "Yes" and "No," a direct route led to "0" and "1." In fact the "0" and the "1" are simply translations of "No" and "Yes." Now we said before that a "Yes" or "No" is synonymous with a "bit." In this case, every "0" or "1" is also an unadulterated, scientifically approved "bit." The "10100" code word for the Jack of Diamonds is accordingly a group of five bits, no more.
We can now also divulge the origin of the word "bit." It is simply a brutal contraction of the two words "binary digit," in other words a step in a binary system. More exactly expressed, a bit is a decisive step that can be represented by a code whose only symbols are "0" and "1."
Phew! This has been quite an exhausting digression. But you now are in on the secret: This is the foundation of electronic life! As for making a practical application of what so far we have been merely using as theoretical exercises...
But no! Let us save that for the next chapter.
The Concise language of the Computer >>>>
©
by PhiloPhax & Lauftext
& Redaktion Lohberg
Kybernetik
- Was ist das?
First printed in Germany: 1963