Ring Cores
First of all we ask you to imagine something again: small curtain rings. (Or, if the ladies prefer, wedding rings.) Rings with a diameter of a sixteenth of an inch or so, made of magnetizable iron oxide, can be dealt with in the same way as a piece of magnetic tape, magnetized with a pulse (though with not more than one per ring), read and extinguished.
So that these rings are easily visible and accessible, they are strong up on a lattice of wires to make a kind of network. We have tried inthe next Illustration to show a portion of such a "ring core matrix." The experts call them "ring cores" instead of simply "rings."
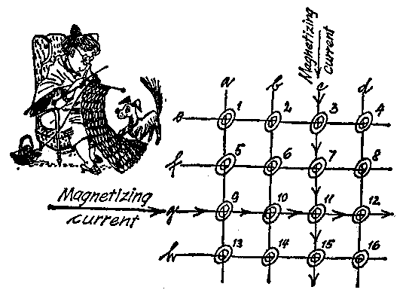
The wires are not only there to keep the rings in piece. They conduct the current whose function it is to magnetize the small pieces of iron. It may already have occurred to you that a magnetized ring means a "1," and an unmagnetized one an "0."
Let us have the ring core numbered 11 in our drawing magnetized from "0" to "1." It is located at the junction of wires "c" and "g." Immediately, we are in a jam. If we send the magnetizing current through wire "c," core 11 will certainly be magnetized, but cores 3, 7 and 15 will be magnetized as well, for they an also threaded on to wire "c." A similar thing will happen if we apply current to wire "g": in addition to core 11, cores 9, 10 and 12 will also be supplied with pulses.
The clever electronics man has found a way out. He divides the magnetizing cement, conducting half of it through wire "c" and the other half through wire "g." Only one of the cores, No. 11, in which the two halfcurrents meet and add up to a complete pulse, will be remagnetized.
In practice, fortunately, the whole procedure takes up less time than we need to describe it.
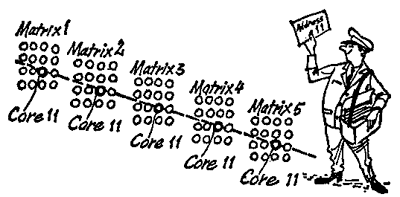
Ring-core matrices are always used in complete groups. An automatic calculator arranged to process numbers with up to seven digits in the 5-channel code will show groups each containing 35 parallel ring-core matrices in its storages. The pulses of each stored seven-digit number (there are 7 times 5 or 35 pulses) are distributed to all 35 matrices. If the number has less than seven digits, a series of ring cores contains nothing at all. The bit of the seven digits of a number will be found in each matrix again in the same place, for example 35 times in each case in ring core No. 11.
There´s nothing to be ashamed of if you find you have to reread that last paragraph again. The theme is complicated. To make it simpler, we shall now assume that we have to deal with an electronic computer which has no numbers to store except one-digit ones - and in the 5-channel code. In this case, we shall only have to deal with five parallel ring-core matrices and not with 35 at a time. Our artist prefers it that way too.
What did we say? The pulses of a number are always stored at the same place, in the same ring core, in every matrix. In our example, ring core 11 would be seen this way:
Addresses >>>>
©
by PhiloPhax & Lauftext
& Redaktion Lohberg
Kybernetik
- Was ist das?
First printed in Germany: 1963